Logistic Regression [coursera 강의 정리]

분류 문제

---

분류 문제는 정답이 0 또는 1 두개의 문제로 볼 수 있다.

 

선형회귀를 사용해서 분류문제를 해결하려고 하면 대부분의 상황에서 정상적으로 동작하지 않는다.

 

그래서 Logistic Regression을 사용하는데 분류문제인데 Regression이 붙는 이유는 역사적(?)으로 그렇게 불렸기 때문이라고 한다.

 

우선 h(x)는 그대로 선형회귀에서 사용했던 모델을 그대로 사용한다. (1차결합 식)

 

다만 g(z)라는 형태로 h(x)를 새롭게 사용하게되는데 g(z)는 sigmoid function이라고도 한다.

 

Logisitic Function의 모양은 위의 그림과 같다. 결과값이 0일때 0.5가 되고 작으면 0으로 수렴하고 크면 1로 수렴한다.

 

쉽게 말하면 선형회귀의 값을 0~1사이의 값으로 만들고 싶고 중간이 되는 지점은 h(x)가 0일때를 말한다.

 

분류를 정하는 방법은 logisitic regression의 결과값이 0.5보다 크면 양성 작으면 음성으로 분류를 하면된다.

 

cost function

---

logistic regressor의 cost function 아래와 같이 정의 된다.

 

선형 회귀의 비용함수를 그대로 적용을 하면 non-convex한 비용함수가 된다.

극소값을 여러개 같게 되므로 비용함수가 0이 되는 지점이 최저점이라고 볼 수 없기 때문이다.

 

그래서 logistic regressor의 비용함수는 log함수를 사용한다. 0~1사이의 값만을 가지므로 비용함수를 그려보면 아래와 같다.

 

convex한 함수이며 미분시 0이 되는 지점이 최소값임이 자명하기 때문이다.

 

두가지 케이스로 비용함수를 설정하는 것보다는 한식에 비용함수를 설정하는것이 더욱 좋기때문에 표현하면 다음과 같다.

y가 0이라면 앞의 항이 날아가고 y가 1이라면 뒤의 항이 날아가기 때문의 같은 효과를 볼 수 있다.

 

비용함수를 설정했으면 이제 경사하강법을 이용해서 파라미터를 업데이트 하는 식은 다음과 같다.

 

선형회귀의 비용함수의 미분과 똑같은 형태를 띄는 것을 확인할 수 있었다.

 

선형회귀와 logisitic regressor 의 차이점은 가설함수의 차이가 있고 y값이 0,1밖에 나오지 않는 다는 점에 있다.

 

Multiclass classification

---

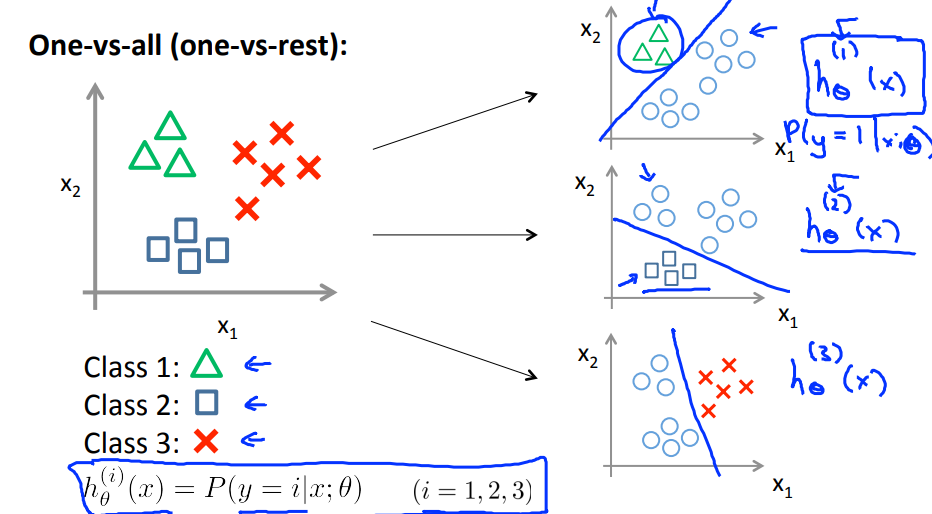
분류를 두개가 아닌 여러개의 클래스를 분류해야한다면 어떻게 해야할까?

 

이진분류는 logisitic regressor에 의해 분류를 할 수 있다. 여러개의 클래스를 분류하기 위해서는 logisitic regressor을 여러개 사용하면 된다.

 

오른쪽 예시처럼 각각의 클래스를 분류하는 모델을 모두 fitting하면 된다.

 

아래의 식에는 y=1이 아닌 i를 변수로 두어 0,1,2,3일때의 확률을 구하고 h(x)에도 i가 첨자로 붙어서 각각의 분류모델을 사용하면된다. 3개의 분류하는 선이 나오고 그중 0.5보다 큰 값을 나타내는 모델이 그 클래스로 분류 할 수 있을 것이다.