-
Linear regressor (선형회귀) Coursera 강의머신러닝 2021. 9. 27. 21:21
선형회귀 개요

입력데이터 x, 결과 값 y가 주어졌을때 분포되어있는 값들을 직선으로 회귀 시키는 것이다.
h(x) 가설 함수라고 한다.

선형함수 회귀식 일차식 y = ax + b의 형태와 똑같다.
주어진 데이터 x,y를 통해 최적의 theta1, theta2를 찾는것을 의미한다.
최적의 theta1, theta2는 어떻게 찾아야할까?
손실함수를 통해 찾을 수 있다.
비용함수(Cost function)
최적의 파라미터를 찾기 위해 비용함수를 사용한다.

오른 쪽 그림처럼 데이터가 있을때 어떤 기울기와 절편을 가진 직선이 최적의 선형회귀 함수라고 할 수 있을까?
당연하게도 실제 값과의 차이가 가장 적은 함수가 최적이라고 볼 수 있다.
그렇다면 그 최적을 찾기위해서는 우선 예측한 회귀 함수와 실제 데이터의 차이를 계산하는 비용함수가 필요하다.

비용함수는 위의 식으로 나타낼 수 있는데 식을 들여다 보면 매우 간단하다.
x,y의 대응되는 값을 집어넣어서 차이를 구한다.
h(x)에 x1을 집어넣고 나온 값과 실제 데이터의 값 y의 차를 구해서 제곱을 한뒤 모든 값의 차를 더한뒤에 m개수로 나눈다.
비용함수의 파라미터 값들을 넣은것을 그래프로 나타내면 다음과 같다.

비용함수 그래프 theta1,theta2의 따른 비용함수의 그래프이다.
이 그래프는 볼록한 convex형태를 띄고 있으며 가장 최소점이 극소점을 나타낸다.
경사 하강법
비용 함수가 최소값을 가지고 있으며 그 값이 선형회귀에 있어서 최적의 파라미터가 된다는 것을 확인 했다.
그렇다면 우리는 그 최소값을 어떻게 찾을 수 있을까? 순서는 다음과 같다.

비용함수가 있고 원하는 목표는 비용함수가 최소가 되는 파라미터를 찾는것이다.
그러기 위해서는 우선 파라미터를 임의의 값으로 초기화를 한다. (예를들면 0,0같은)
비용함수가 작아지는 방향으로 파라미터들을 바꿔주면서 마지막에는 최소가 되는 값이 되면 된다.
아무렇게나 값을 바꾸면 최소값은 영원히 찾지 못할 것이다. 최소값을 찾는것에도 방향이 필요하다.
그러기 위해 미분을 사용한다.

비용 함수 J에 대해 미분값에 alpha를 곱한 값을 원래의 파라미터 theta_j에 대해 빼서 새로운 theta_j를 구한다.
각각의 파라미터에 미분 식을 쓰면 다음과 같다.

이제 파라미터를 찾기 위해 변수의 우리가 알고 있는 값을 대입만 해주면서 업데이트만 해주면된다.
하지만 이때 아직 모르는 값 하나가 남아있다. alpha이며 alpha는 learning rate(학습률)이다. 얼마만큼 값을 업데이트 하는지를 결정한다.
학습률이 너무 큰경우, 작은 경우 모두 문제가 있다.
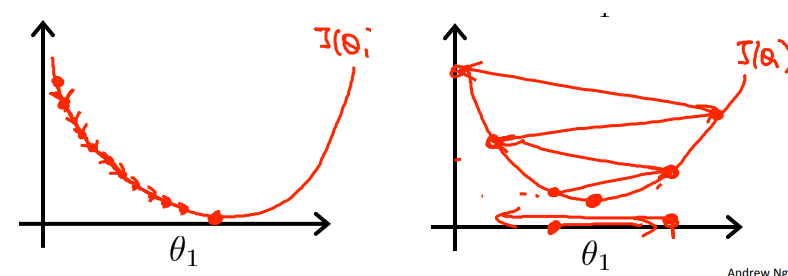
학습률이 너무 작게 설정되면 최소값으로 가는데에 시간이 너무 오래걸린다.
안그래도 최소값으로 갈수록 업데이트 되는 범위가 점점 작아지는데 시작부터 작게 출발하면 오래걸릴 것이다.
너무 크게되면 최소값에 도달하지 못하고 좌우를 반복해서 움직일 것이다.
학습률을 어떻게 설정하는지는 중요한 문제이다.
요약

선형회귀 함수가 있고 선형회귀 함수를 구성하는 파라미터는 비용함수를 통해 구한다.
비용함수가 최소값이 되는 theta1, theta2를 구하기 위해 경사하강법을 사용하고 경사하강법은 미분값을 이용하고 학습률을 곱해서 값을 갱신해서 업데이트 해간다.
'머신러닝' 카테고리의 다른 글
Logistic Regression 정리 (0) 2021.10.12 Logistic Regression [coursera 강의 정리] (0) 2021.10.05 Normal eqation coursera 강의 정리 (0) 2021.10.04